基本初等函数
正比例函数
反比例函数
一次函数
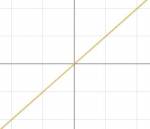
当未知数x的次数为1时,称为一次函数。标准形式为 。与正反比例函数很相似,当b=0时,为正反比例函数。
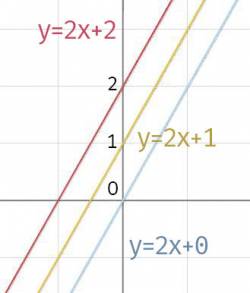
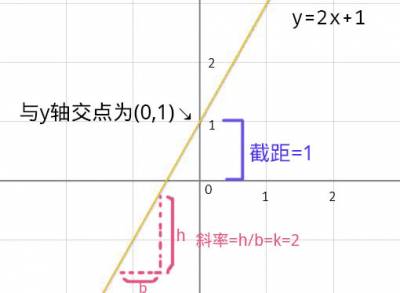
一次函数中的常数项b的几何意义是将函数上下平移b。因为正比例函数是过原点的,当上下平移b单位个之后,函数与y轴的交点为(0,b)。我们把函数与y轴相交的点到原点的距离称为截距。那么一次函数的截距为b
下面是一次函数的性质:
- 一次函数是一条直线
- 一次函数与y轴的截距为b
- 一次函数斜率为k
- 一次函数单调,增减由k决定
- k为0时,不是一次函数
二次函数
二次函数,又称抛物线,图形是一条抛物线,也就是往空总抛东西的运动轨迹。
标准形式为
为什么抛的东西就是这样的轨迹呢,我们可以把抛物运动分为两个方向,一个是水平向前,一个是垂直向上,两个运动结合起来就是抛物运动。
把东西扔出去后,物体只受到重力的作用,所以水平方向上没有力,速度就不变,就像函数的x一样是均匀变大的。而在竖直方向上,物体就像我们原地往上扔东西一样,先上升,再下降,就像函数的y轴,由x²决定,x²并不是均匀的。两者结合起来就是抛物线的样子。
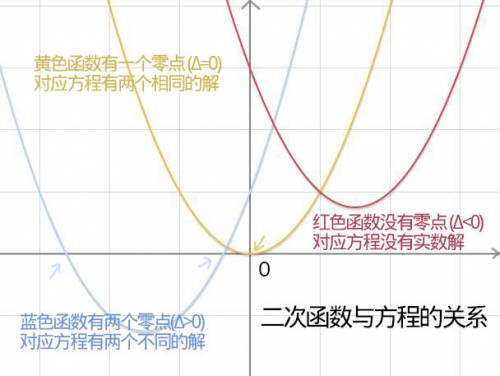
 抛物线的性质:
抛物线的性质:
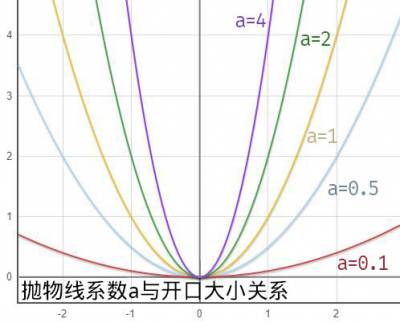
抛物线开口向上
抛物线开口向下
- a越大,开口越小;a越小,开口越大
时,为偶函数
- 抛物线中心对称线横坐标
幂函数
形如 ,a为有理数的函数称为幂函数,上面的
即是幂函数的一种。
幂函数中指数a的不同对函数性质有较大的影响,这里不一一讨论,只列出一些简单的规律:
时,函数必过(0,0)和(1,1)
时,函数必过(1,1)
时,函数不是直线,在(0,1)处有断点,因为
无意义
指数函数
形如 的函数称为为指数函数,即底数不变为常数,指数为自变量的函数。指数函数是非常重要的函数,很多自然现象都与它有关。例如一个细胞一分钟能分裂成两个,两分钟分裂成四个,然后八个、十六个、三十二个……要描述细胞的数量,我们可以用函数
来表示,x代表的是一共分裂了多少分钟。
讨论指数函数,我们可以按照a的取值来分情况:
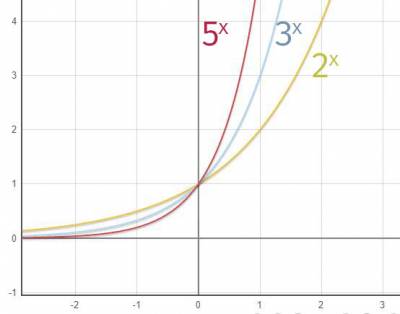
当a>1时
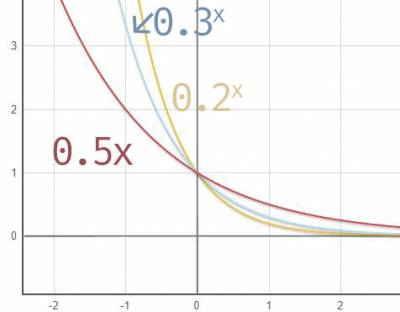
当0>a>1时
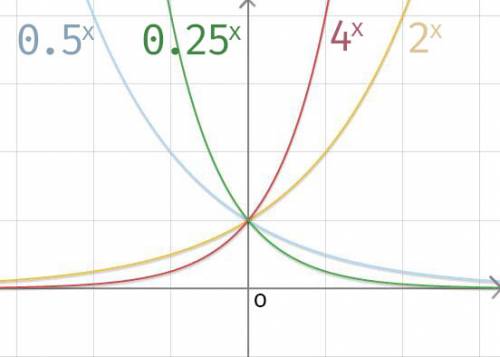
对称性
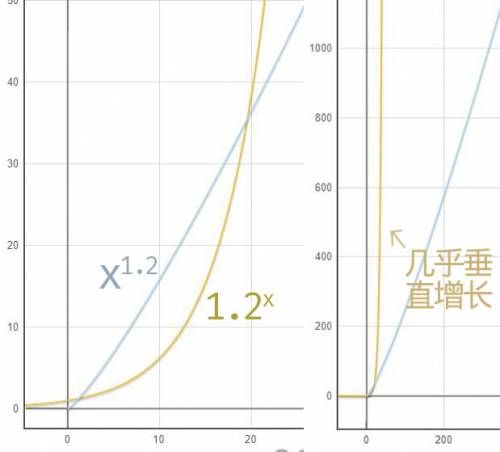
指数式增长
指数函数的增长速度非常快。如果一个细胞一分钟分裂成两个,一个小时就能分裂出个,把这个数写开也就是
个细胞。所以我们一般形容某样东西数量增长很快就会用指数增长或指数式增长来形容。
下面图片是相同的a情况下,指数函数与幂函数的对比。缩小之后可以看到指数函数近乎垂直增长
对数函数
形如 的函数称为对数函数,对数和指数是一对互为逆运算的运算符,所以他们的函数之间有许多相似的地方。
对数函数的定义域为 x>0
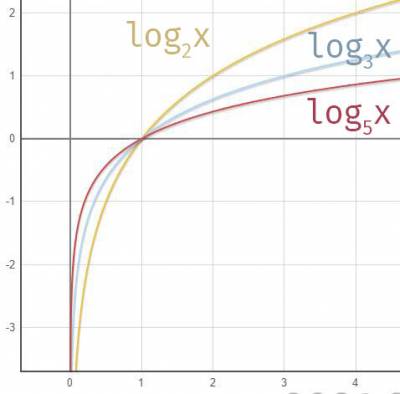
当a>1时
当0>a>1时
指数函数与对数函数的关系
指数运算和对数运算互为逆运算,所以函数间也有一定的关系:
| 指数函数 | 对数函数 | |
|---|---|---|
| 形式 | | |
| 定义域 | R | |
| 值域 | | R |
| 必经点 | (0,1) | (1,0) |
| | 增长 | 增长 |
| | 减少 | 减少 |
可以看出指数函数和对数函数存在许多对称关系,甚至当a相同时,指数函数还与对数函数沿对称:
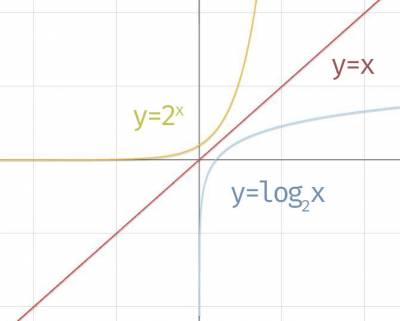
三角函数
三角函数内容较多,另开页面编写,完成后在此附上链接